| Contenu | |
| De quelles mathématiques aurai-je besoin à l'université? | |
| Qu'est-ce que le calcul différentiel et intégral? | |
| Pourquoi le calcul différentiel et intégral est-il important? | |
| De quels préalables ai-je besoin? | |
| En quoi consiste un cours de calcul différentiel et intégral à l'université? | |
| À L'AIDE! Je dois passer un test de classement! | |
| À L'AIDE! On veut m'enlever ma calculatrice! | |
|
Obtenir la brochure "Préparation au calcul différentiel et intégral à l'université" |
|
| Télécharger la brochure en format pdf | Pour lire les fichiers .pdf
|
|
Read this in ENGLISH |
|
Certains départements (autres que les mathématiques) peuvent offrir leurs propres cours de calcul différentiel et intégral, d'algèbre linéaire ou de statistique. Dans ce cas, vous ne serez peut-être pas tenu de suivre les cours standards de première année proposés par le département de mathématiques.
Les notions de base du calcul différentiel et intégral englobent la limite, la dérivée et l'intégrale. La dérivée d'une fonction est son taux de variation instantané en rapport une autre variable. Ainsi, la dérivée de la hauteur (en rapport avec la position) est la pente ; la dérivée de la position (en rapport avec le temps) est la vélocité; et la dérivée de la vélocité (en rapport avec le temps) est l'accélération.
L'intégrale d'une fonction peut être perçue par exemple comme étant l'aire se trouvant sous son graphe ou comme une sorte de total en fonction du temps. Ainsi, l'intégrale de la pente est (à une constante près) la hauteur; l'intégrale de la vélocité est (à une constante près) la position et l'intégrale de l'accélération (en rapport avec le temps) est la vélocité. Comme vous l'aurez peut-être deviné, les intégrales et les dérivées sont reliées et, dans un sens, opposées.
De nombreuses fonctions, mais pas toutes, peuvent être représentées
par des expressions algébriques. Par exemple, l'aire d'un cercle est reliée à son rayon par
la formule A = 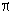 r2, et la distance sur laquelle un corps tombe dans un temps t,
en démarrant immobile, s'exprime comme suit : x = 1/2 at2. Par de telles expressions,
le calcul différentiel et intégral nous permet de trouver des expressions pour
l'intégrale et la dérivée de la fonction, quand elles existent.
r2, et la distance sur laquelle un corps tombe dans un temps t,
en démarrant immobile, s'exprime comme suit : x = 1/2 at2. Par de telles expressions,
le calcul différentiel et intégral nous permet de trouver des expressions pour
l'intégrale et la dérivée de la fonction, quand elles existent.
La physique, l'astronomie, les mathématiques et le génie sont des domaines où le calcul différentiel et intégral joue un rôle primordial; on peut difficilement voir comment une seule de ces disciplines existerait dans sa forme moderne sans le calcul différentiel et intégral. Toutefois, la biologie, la chimie, l'économie, l'informatique et d'autres sciences utilisent aussi le calcul différentiel et intégral. De nombreuses facultés de sciences exigent donc que tous leurs étudiants suivent un cours de calcul différentiel et intégral; dans d'autres cas, l'étudiant pourra peut-être choisir entre un cours de calcul différentiel et intégral, de statistique et d'informatique, par exemple.
Il faut bien comprendre que les mathématiques ne se limitent pas au calcul différentiel et intégral. L'algèbre linéaire, la probabilité, la géométrie et la combinatoire ne sont que quelques-unes des branches des mathématiques abordées dans les écoles qui sont importantes au niveau universitaire. Les compétences en matière de résolution de problèmes, qui touchent toutes les branches des mathématiques, permettent d'appliquer cette discipline à d'autres sujets.
Vous ne pourrez réussir ce cours en vous contentant de mémoriser toute la matière; il vous faudra aussi la comprendre, chose qui ne se produira pas instantanément et que le maître ne pourra pas faire à votre place. Vous devrez faire des efforts soutenus et participer activement au cours. Si vous travaillez avec constance jusqu'à la fin, vous serez récompensé de vos efforts.
La matière du cours se compose d'un nombre plutôt restreint de grands principes et d'un nombre modéré de formules que vous devrez savoir et non de centaines de raccourcis et de règles particulières. Les étudiants font souvent l'erreur, particulièrement en ce qui a trait aux problèmes sous forme d'énoncé, d'essayer d'apprendre une règle pour chaque type de problème. Ne faites pas ça; essayez plutôt de comprendre les divers éléments des problèmes.
Voici les étapes d'apprentissage et de maîtrise d'une nouvelle notion de calcul différentiel et intégral:
 | Vous-même. Si vous prenez du retard et n'étudiez pas assez - disons de cinq à six heures par semaine hors de la classe pour chaque cours, mettez-vous vite au travail et ouvrez votre manuel. |
 | Votre manuel renferme des centaines d'exemples de résolutions de problèmes et des milliers de problèmes. Habituellement, on trouve les réponses à près de la moitié des problèmes au dos du livre. Vous pourriez aussi vous procurer un guide d'études montrant en détail la façon de travailler ces problèmes. Vous pouvez aussi acheter d'autres livres comme les manuels de la série Schaum , qui renferme aussi des résolutions de problème. |
 | Vous pourrez durant les heures d'accueil aller voir votre professeur pour obtenir de l'aide. Essayez de déterminer à l'avance ce qu'il peut vous aider à comprendre de façon à mieux profiter de la rencontre. |
 | Vous pouvez aussi discuter de votre problème avec vos camarades, ce qui n'est pas la même chose, bien entendu, que de copier leurs travaux. à l'université, des peines sévères, dont l'expulsion parfois, sont imposées aux étudiants qui trichent. |
 | Vous pourriez aussi engager un tuteur . Toutefois, ne lui demandez pas de faire vos travaux pour vous; n'oubliez pas qu'il ne pourra pas vous accompagner à l'examen. Demandez-lui plutôt de s'assurer que vous comprenez la matière. |
 | Votre université dispose peut-être d'un centre d'aide en mathématiques , et offre sans doute aussi des séances d'enseignement tutoriel en groupe ou d'autres ressources. à vous d'en profiter! |
 | Il est possible que votre université ou votre syndicat d'étudiant organise des ateliers sur la manière d'étudier et de prendre des notes efficacement, de faire face au stress des examens, etc. Vous pourrez aussi bénéficier de conseils pour d'autres problèmes pouvant nuire à vos études. |
Ces mesures visent à empêcher les étudiants d'aborder le calcul différentiel et intégral sans être adéquatement préparés, puis de prendre du retard et d'échouer. L'expérience a montré que la plupart des étudiants qui abordent le calcul différentiel et intégral sans être suffisamment préparés échouent effectivement.
Le test de classement est souvent à choix multiples de façon à pouvoir noter l'étudiant le plus rapidement possible. L'utilisation de manuels ou d'une calculatrice n'est généralement pas permise (voir la section suivante). Comme il faut être passablement bien préparé pour réussir la première année de calcul différentiel et intégral et que le test de classement porte sur une matière très élémentaire, mais importante, la note de passage peut être supérieure à 50%. Vous devrez probablement passer ce test au début ou avant le début du semestre; renseignez-vous à l'avance sur le règlement en vigueur dans l'université que vous prévoyez fréquenter.
 |
Si vous ne pouvez utiliser votre calculatrice dans votre cours de calcul différentiel
et intégral, les questions seront posées de façon que vous n'en ayez pas besoin
pour répondre. Le professeur ne peut raisonnablement vous demander de calculer |
 |
Si l'utilisation de la calculatrice n'est pas permise, toute expression n'ayant pas une
simplification bien connue peut toujours être laissée telle quelle. Ainsi,
bien que vous devriez savoir que 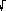 25 = 5, et que log10 1000 = 3, vous pouvez
toujours laisser, par exemple, 25 = 5, et que log10 1000 = 3, vous pouvez
toujours laisser, par exemple, 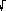 17 ou ln(1000) telles quelles, ce qui est encore plus facile que d'utiliser une calculatrice. 17 ou ln(1000) telles quelles, ce qui est encore plus facile que d'utiliser une calculatrice. |
 |
Notez toutefois qu'on s'attendra
généralement à ce que vous simplifiez, par exemple, 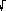 17/ 17/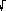 17 17 |
 |
Même si vous ne pouvez utiliser une calculatrice dans votre cours de calcul
différentiel et intégral, on vous demandera souvent de répondre par
une expression algébrique comportant des nombres entiers. Par exemple, on pourrait
vous demander ceci : `` Répondez par une expression de la forme 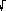 b/c où b et
c sont des nombres entiers.'' Il est beaucoup plus important dans le calcul différentiel et intégral de savoir
que sin( b/c où b et
c sont des nombres entiers.'' Il est beaucoup plus important dans le calcul différentiel et intégral de savoir
que sin(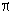 /4) = /4) = 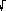 2 / 2 que de savoir que c'est approximativement égal à 0.707. 2 / 2 que de savoir que c'est approximativement égal à 0.707.
|
| Pour nous faire part de commentaires ou d'erreurs sur la page WEB, veuillez contacter Robert Dawson. Par ailleurs pour d'autres précisions, vous pouvez contacter le département de mathématiques de l'université concerné. | |
Départments participant |
|
| Acadia University, Department of Mathematics and Statistics | |
| Dalhousie University, Department of Mathematics, Statistics and Computing Science | |
| Mount Saint Vincent University | |
| Saint Marys University, Department of Mathematics and Computing Science | |
| Memorial University of Newfoundland, Department of Mathematics and Statistics | |
| Sir Wilfred Grenfell College, Department of Mathematics | |
| Saint Francis Xavier University, Department of Mathematics, Statistics and Computer Science | |
| University College of Cape Breton | |
| University of New Brunswick (Fredericton), Department of Mathematics and Statistics | |
| University of New Brunswick (Saint John) | |
| Université de Moncton | |
| University of Prince Edward Island, Department of Mathematics and Statistics | |