1. A problem is algorithmically solvable, if a computer program
can be written that will produce the correct answer for any input
if we let it run long enough and provide as much storage space
as necessary.
2. Numerous problems with practical applications can be algorithmically
solved. However, the time and space requirements of these programs
is of practical importance. Study of these requirements is one
of the important areas in computer science called computational
complexity or algorithm analysis.
3. How does one calculate time requirements?
a priori estimates
a posteriori testing
For a priori estimates of actual execution time, we need to know
the details about the machine and will not be valid for another
machine. Multiprogramming or time sharing makes these estimations
even more difficult.
Hence, we generally deal with the frequency counts of number
of instructions that will be executed. Consider the following
three cases.
{ // a
x++;
}
{ //b
for( i = 0; i < n; i++)
x++;
}
{//c
for( i = 0; i < n; i++)
for( j = 0; j < n; j++)
x++;
}
{//d
for( i = 0; i < n; i++)
for( j = 0; j < i; j++)
x++;
}
In (a), instruction x++ is executed only once.
In (b), instruction x++ is executed n times.
In (c), instruction x++ is executed n^2 times.
Finding out how many times each instruction in a large program
is run can also be a tedious task.
· Find out the key instructions in a given algorithm. Key instructions are those that simply cannot be avoided.
· For example, comparison operation in searching problems is the key operation.
· Generally, the key operation will be the one which is most frequently executed.
· Find the frequency of execution of the key step.
· Finding the frequency can be difficult for a complicated algorithm
· Comparisons of different algorithms
based on frequency may not necessarily be worthwhile.
One algorithm executes the key step 100*n+234
Other algorithm executes the key step n**2 times
Which algorithm is faster?
Depends on the value of n.
If we are dealing with very large values of n (a generic
term for size of input), then 1, n, n2 are said to be in different
classes and are in increasing orders of magnitude.
We are interested in the order of magnitudes for an algorithm.
This means determining those (key) statements which may have the
greatest frequency count.
DEFINITION: f(n) = O(g(n)) if and only if there exists two constants c and N such that |f(n)| >= c|g(n)| for all n N.
We write O(1) to mean a computing time which is a constant.
O(n) is called linear.
O(n^2) is called quadratic.
O(n^3) is called cubic.
O(2^n) is called exponential.
For large n, the time requirements are:
O(1)<O(log n) < O(n) < O(n log n) < O(n^2) <
O(n^3) << O(2^n)
These seven computing times are the ones, which are seen most often in practice.
Given an algorithm, we analyze the frequency count of each statement
and total the sum. This may give a polynomial
where ck != 0 and n is a parameter. Using bigoh notation, P(n) = O(nk). On the other hand, if any step is executed 2n times or more the expression
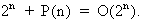
Another valid performance measure is the space requirements is the space requirements. Often one can trade space for time, getting faster algorithm but using more space. Space can also be measured using bigoh notations.