• A computer program that emulates the behaviour of a human expert who is involved in solving problems associated with a particular domain of knowledge.
  • Restricted to a given domain
• Early expert systems hard coded a body of knowledge as well as inferencing mechanism
• Since then the technology has evolved. Expert system consists of three modules
  • Knowledge base
  • Inference engine
  • User interface
• Separation of knowledge from inference engine allows us to build, upgrade the knowledge easily
• This concept is not new we have already seen that when we worked with logic
• A typical expert system should have the following features:
  • Deal with uncertainty
  • Explanation (how the system arrived at the conclusions)
  • Ease of modification (easy to modify the knowledge base)
  • Transportable to different platforms
  • Adaptive learning: Learn rules on its own.
• Areas of applications
• Control: Operate an entire system of equipment on its own.
• Debugging: If a system is not realizing its potential, then figure out the problems and provide possible solutions.
• Diagnosis: Similar to debugging but do not suggest solutions.
• Repair: Similar to debugging but goes one step further and carries out the solution.
• Design: CAD/CAM applications.
• Instructions: Education application
• Interpretation: Given a massive volume of data/information.
• Planning: Will be discussed in greater detail later on.
• Prediction: We will talk about this more in the context of neural networks.
• Examples:
  • MYCIN (medicine), Dendral (chemistry) both came from Stanford. One of the main researchers Feigenbaum.
  • Prospector (Geology)
  • YESMVS

• Production rules
  • IF (antecedent/situation/premise) THEN

(consequent/action/conclusion)

• Not much different from Prolog
• But most expert systems allow you to add a numeric value generally referred to as a Certainty Factor
• The obvious limitation is that experts may or may not be able to summarize their knowledge in terms of IF...THEN rules
• Simple, easy to understand and maintain a knowledge base.

• Semantic networks
  • Nodes that represent objects, concepts or events
  • The arcs can define various relationships between the nodes
  • See the example from the blackboard
  • Of course, the program is not going to be using the semantic networks as shown in the picture. The actual data structure will depend on the software package.
  • The actual inferencing will start from a node in the semantic net and use various search techniques and pattern matching to arrive at the conclusion
  • The general principle is similar to the logic inferencing
  • The difference is that you have more expressive power
  • Disadvantage is that the networks can be extremely complicated to build and maintain
• Frames
  • Similar to the objects in OOP
  • Generally combined with other knowledge representations such as production rules and semantic nets
  • Frames may allow us to divide a knowledge base into a subset
  • Frame may consists of production rules relevant to a particular subdomain
  • Searching for the solution involves two steps. Locate the appropriate frame and then carry out the usual inferencing.
  • A frame has two parts: a name and a set of attributes associated with each part

Slot name	Filler
Frame name	Immediate family
Father	John
Mother	Sue
Sister-1	Judy
Sister-2	Jill
Brother	nil

• You can also associate various procedures with a slot. The procedures are triggered depending upon the available facts.
• For example, if we have a frame defined for a trip with slots such as destination and as soon as the user says I want to take a trip. The frame for the trip will be created and the destination slot will trigger and input routine. The cost slot will trigger a routine to find best possible cost and eventually produce a complete travel itinerary.
• First-order logic is another possible representation for the expert systems
• Production rules
  • MYCIN was hard coded
  • The success of MYCIN prompted the developers to come up with a shell called EMYCIN
  • A shell has a (choice of) built-in inferencing mechanisms.
  • The developer builds the knowledge base and develops an user interface. Involves limited amount of programming.
  • A very old copy of an expert system called Guru can be accessed in the labs by typing goguru.
• Forward chaining and backward chaining
  • Forward chaining starts with the facts and finds conclusions
  • Backward chaining starts with what we want to know and tries to figure out if we have necessary facts.
• Inferencing with certainty factors
  • MYCIN certainty factors
  • The certainty factors are used as thresholds for firing the rules and they are also used to qualify the conclusion.
  • IF E1 (threshold CF1) THEN C1 (CF = CF2).
  • The rule will not be fired if our belief in E1 is less than CF1. If the belief in E1 is say CF3 then we will conclude C1 with CF2*CF3.
  • IF cough THEN flue (CF = 0.8). The certainty factor for cough is 0.9 then certainty for flue will 0.8*0.9=0.72.
  • The certainty factors in MYCIN are between -1 and 1. They are calculated from probabilities called measure of belief (mB) and disbelief (mD)
  • CF(H,E) = mB(H,E) - mD(H,E), where (H,E) means hypothesis given the evidence E.
  • This formula gave too much weightage to the mD. For example, mB(H,E) = 0.8 and mD(H,E)=0.6 then CF=0.2.
• CF(H,E)=(mB(H,E)-mD(H,E))/(1-min(mB(H,E),mD(H,E))
• The calculations of CF are adhoc.
• IF E1 and E2 and E3 THEN C1 with CF=CF1
• if E1 has CF2 E2 has CF3 E3 has CF4 what is the confidence in C1.
  • min(CF2,CF3,CF4)*CF1
  • avg(CF2,CF3,CF4)*CF1
  • what happens if we had or connective instead of and: One possibility is to replace min with max
  • Depends on the system designer
• Handling uncertainty is adhoc
• Cannot really say that the CF generated using one scheme are better than the other.
• Fuzzy logic
• Fuzzy set theory
• Extension of the set theory
• An element does not crisply belong or doesn't belong to a set. An element has a degree of membership to a set. The membership value is in [0,1]
• A={(e1,m1), (e2,m2),......,(en,mn)}
• A conventional set has membership values of either 0 or 1.
• {e1,e2,e7,e8}
• {(e1,1),(e2,1),(e3,0),......,(e6,0),(e7,1),(e8,1)}
• Generalization: A theory can be generalized in many different ways. A generalization means that the old theory can be shown to be a special case of the new theory with certain assumptions. Any conclusion drawn from old theory should also hold in the new theory.
• Another example of generalization of sets is bags. bags allow duplicates.
• Fuzzy set theory has corresponding operations for all the set theoretic operations.
• Fuzzy inferencing in the rule based expert systems.

• The fuzzy controller of a car's air conditioner might include rules such as:
• If the temperature is cool, then set the motor speed on slow.
• If the temperature is just right, then set the motor speed on medium.
• If the temperature is warm, then set the motor speed on fast.
  • Here temperature and motor speed are represented using fuzzy sets.
  • Each temperature is represented by a fuzzy set calculated using a membership function.

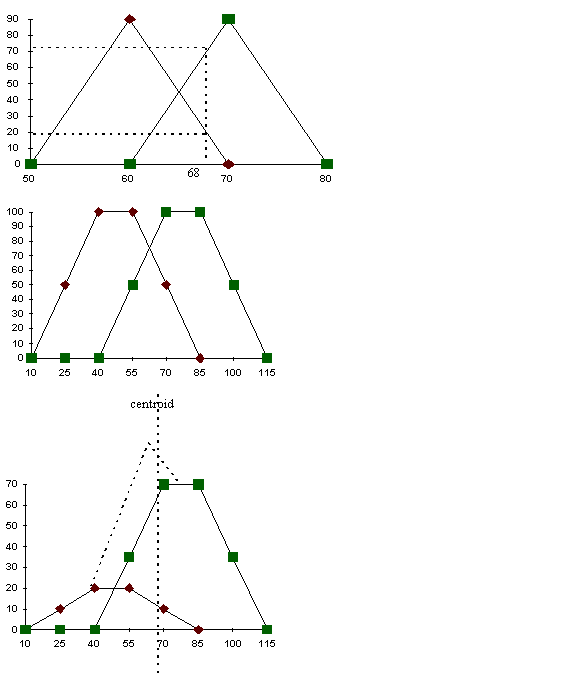
• For example, 68 F is represented by the set
• {(cold,0), (cool,0.2),(just right, 0.7)(warm,0),(hot,0)}
• Two rules that will be fired will give us slow with 0.2 and medium with 0.7 memberships.
• This fuzzy sets needs to be converted to a crisp motor speed.
• So, the graph for slow is shrunk by 0.2 and the graph for medium is shrunk by 0.7. The centroid for the combined graph gives us the motor speed.
• Definitely more complicated than the CF1*CF2 that we used with certainty factors
• Proven to be useful for simple controllers such as cameras, washing machines, subways, etc. Mostly in Japan.
• Researchers say that with more complicated knowledge base, this inference mechanism will not (does not) work well.