Data Abstraction and Problem Solving with C++

Walls and Mirrors

Verification: Examples of loop invariants.

The for loop on j computes 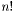$n!$ for an integer $n \geq 0$

Confirm that the following invariant holds on the for loop:

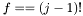
The while loop computes an approximation to 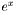$e^{x}$ for a real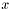 $x$

Confirm that the following invariant holds on the while loop:

Invariant:

$t == \frac{x^{(k-1)}}{(k-1)!}$

and

$s == 1 + x + \frac{x^{2}}{2!} + \dots + \frac{x^{(k-1)}}{(k-1)!}$

Definition in file c01p032.cpp.

Generated on Sat Aug 26 19:58:10 2006 for

1.4.6