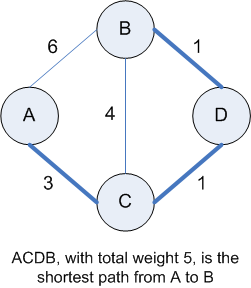
For a connected, weighted graph, a shortest-path algorithm finds, for any two vertices, the sequence of edges between them having the smallest total weight, as illustrated in the following diagram:

You might think that you could just take the minimum spanning tree of a graph, or part of it (after removing some edges) to get the shortest path, but we can see that this won't work by looking at the following example:
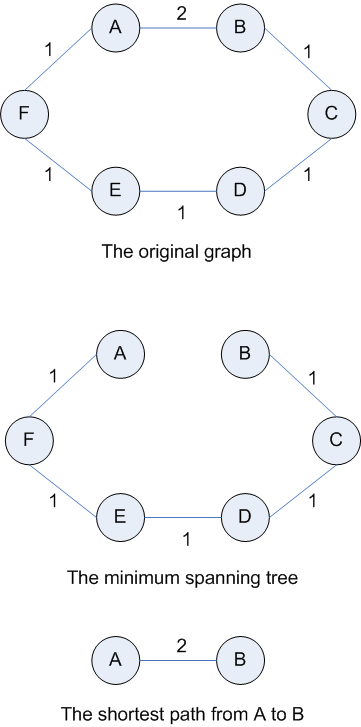
The reason the previous "greedy" algorithm for finding the minimum spanning tree doesn't work for shortest paths is that it considers only the weight of a single edge when choosing a new vertex to add on each pass. Thus we need to modify that algorithm so that it chooses the edge to the fringe that is part of the shortest entire path from the starting vertex.
Algorithm FindShortestPath
--------------------------
Select a starting vertex
Build initial fringe of all vertices adjacent to starting vertex
while we have not yet reached the destination vertex
Find "fringe edge" with shortest path to starting vertex
Add associated vertex and edge to the shortest path
Update fringe as follows:
Add to fringe all vertices connected to new vertex
for each node in the fringe
Update its edge to the one giving shortest path to starting vertex