Hashing
Suppose the name John and some information about him is stored in a vector. How do we we retrieve this information? Quite easily, if we know the index at which it's stored, which is highly unlikely. Otherwise we have to search through the vector till we find John. What if the information is stored in a list? In this case we have no index and have to search anyway. What if it's in a binary search tree? Again, no direct access, so we have to chug down the tree, going this way and that, till we find John.
Suppose, instead, we had a structure that worked like this: As soon as we know we're looking for John, we know where to go to find him. Going back to the vector, for example, instead of putting John at some arbitrary location whose index we will not remember past breakfast tomorrow, we actually use John's name as the input to a function that calculates the index where we store John and his information. Then all we have to remember is what calculation we used and the next time we want John's information we perform the same calculation on John and it gives us the same result (the same index) so we simply go directly there to find John's information. And, of course, if we're storing Mary's information we use the same calculation to determine where it should go as well. In other words, we use the same calculation for everyone.
That's "hashing", so-called because the kinds of functions we use to transform names into indices tend to "chop up" or "make hash of" the names to produce the indices of the required storage locations.
At least that's the basic idea of hashing. As you are well aware by now, there's no free lunch, so hashing is not going to be the solution to all our storage and information retrieval problems. You can probably already think of some things that might go wrong. What happens, for example, if two different names want to be stored in the same location. That is, what problems are caused if our "hashing function" is not one-to-one? This is typical of the sort of problem that arises in hashing and that must be dealt with appropriately.
What exactly do we mean by "table lookup"? A "table" is generally a two-dimensional rectangular structure with "rows" and "columns", but in this wider context we can think of it as having other shapes, such as "upper triangular", "lower triangular", or even "jagged". We could even think of a one-dimensional structure such as an array or vector as a kind of "degenerate table" in this context. In any case, all of these structures provide direct access to their contents via one or more indices that we use to "look up a value in the table". Often the indices are simply integers, but they don't have to be.
Here are some examples of "tables":
Even these few examples confirm a couple of things:
A nice thing about table lookup is that it's very fast. In fact, when we have the index location of an item, the lookup is O(1), or a constant time operation. That is, we go directly to the value, and hence the performance does not depend on how many data items are stored. For the sake of comparison, look at the following table:
| table lookup | O(1) |
| contiguous storage, unsorted | O(n) |
| contiguous storage, sorted | O(log n) |
| singly-linked storage, sorted or unsorted | O(n) |
| linked storage, BST | O(log n) |
However, even though table lookup is generally very fast, the problem of finding the index of a place to store a given item is not an easy one.
The process of searching for a data item in any container of data items can always be viewed as a hunt for the function f in the following diagram:

Note that assuming f is one-to-one (x≠y ⇒ f(x)≠f(y)) is equivalent to assuming that each data item has only one key and items with different keys will be found in different locations. If f is also an onto function, this would mean that all the data locations are actually occupied. The question of whether our "hashing functions" are "one-to-one" and/or "onto" are ones that we need to think about when searching for such functions. The ideal hashing function is, of course, one that is both one-to-one and onto.
Thus the central problem that hashing deals with is this: What do we do if the key itself (or some simple, one-to-one and onto arithmetical function of the key) cannot be used directly as an index into contiguous storage, but we still want to use the key to go directly to a memory location in O(1) time?
And, since suitable one-to-one, onto functions are usually impossible to find (or at least so difficult to find that we don't bother to search) the associated questions revolve around the problems caused by the lack of such a function, and how we overcome those difficulties.
Suppose we want to store a list of famous people and use each person's birthdate as a key in such a way that, given a date, we can find "the" person born on that date in O(1) time. [Can you think of any reasons why we might have enclosed "the" in those quotation marks?] This example will give us an opportunity to apply the basic principles of hashing by attempting to find a suitable hashing function, to see what problems arise, and to examine some approaches to dealing with them.
So, our data might look like that illustrated in this table:
| Key (date) | Data Value (name) |
|---|---|
| 12/31/65 | Joe Blow |
| 01/01/36 | Mary Roe |
Note that the date is given in the usual form used in the USA, which is not, unfortunately, the most convenient way to represent dates. However, quite often we must deal with data in the form in which it is given to us, however inconvenient that form may be.
In any case, on this occasion, we next need a function f such that
f(key) = index_of_location_where_key_and_data_values_will_be_stored
or f(date) = index_of_location_where_date_and_name_will_be_stored
and if this is a one-to-one onto function, we're home free. But, as we intimated above, this is not likely to be the case.
We could use a function that simply does this ...
f(12/31/65) = 123165
f(01/01/36) = 10136
and so on ...
That is, we could simply discard the forward slashes that appear in the date, and use the resulting number as a table index (array or vector index, say). However, there are at least two problems with this approach in this example, and, from a pedagogical standpoint, fortunately these two problems are quite typical of the kinds of problems that arise in hashing. So, looking at how we might deal with them here will be useful in a wider context.
With this approach, we would need over 100,000 storage locations, even if we only had 1000 names to store. This kind of situation is described by saying that the data is sparse in the storage, and is characterized by wasteful use of storage.
Thus the "obvious" hash function is unsatisfactory and we should seek one that generates a more compact range of index values that span a much smaller index range.
What if two or more famous people have the same birthdate? Then, even with all that empty space, we will be trying to put two (or more) names into the same storage location. This is called a collision (a "hash clash"), and is one of the classic hashing difficulties. A hash function that does not permit collisions is called a perfect hash function, and clearly must be one-to-one.
In practice, most hash functions do cause collisions, and many different methods have been devised to "resolve" these collisions. Thus the term collision resolution refers to any scheme used to find a new location for storing a data item when the "natural" location that it would occupy is already taken.
Suppose we choose a table size (array size or vector size) at least large enough to hold the data, and perhaps with a little to spare, but not too much larger. Let's call this value TABLE_SIZE, and then, to calculate an index for storage, use a function of the form
index = f(date) = date_without_slashes % TABLE_SIZE
in which the modulus operation guarantees an index lying within the range of indices of the table. Also, choosing TABLE_SIZE to be a prime tends to distribute the items more evenly, but it does not guarantee that there will be no collisions. For example, even if we have only 80 names and choose TABLE_SIZE to be 97, then
11/02/14 -> 110214 % 97 = 22
10/03/57 -> 100357 % 97 = 59
04/27/32 -> 42732 % 97 = 52
05/14/32 -> 52432 % 97 = 22
shows us that collisions can easily occur, even though the birthdates are about 18 years apart. When such a collision occurs, we have to perform a rehash to find a new location for the second entry, and hence "resolve the collision".
Thus this second "possible solution" is an improvement over the first in that the storage requirements are much more reasonable, but we have not dealt with the second problem of potential collisions. In fact, we may have exacerbated it, since by having much less storage, there may be a greater chance of collisions occurring.
By now it should be clear that in choosing or creating a hash function we apply two broad criteria:
Here is one typical technique for constructing a hash function:
We will just look at this way of resolving collisions when hashing:
Before we discuss the above strategy for collision resolution in detail, we should point out that this whole problem of collisions and their resolution is what leads to the degradation of performance in hash table solutions. Remember that the whole idea behind hashing is that it should give us a way to retrieve any data item by going directly to the storage location where that item is stored (in O(1) time).
However, when we have had collisions, and resolved them, what does this mean? It means that when we go directly to the location to which a key and the hash function calculation send us, the item we're seeking may not be there, and we therefore have to follow the path determined by the collision resolution process, checking each item along the way, till we find the one we actually want. Of course, another goal in hashing is to minimize the maximum length of any of these additional paths for any given hashing scheme.
In this method, we begin by assigning an unused table location to the first element that claims it. Any subsequent element that maps to the same location is stored in another location whose address is determined by a "re-hash" function, that is, a function which takes as input the storage location that is already occupied and uses it to calculate another (possible) storage location. This location might be occupied as well, in which case the process will have to be repeated once more, and for as many times as it takes to find a location or run out of places to look. Note that "running out of places to look" can happen for at least two distinct reasons:
One common type of "re-hash" function takes the form:
new_index = (old_index + 1) % TABLE_SIZE
or, more generally,
new_index = (old_index + k) % TABLE_SIZE
in which the value k (or 1, as the case may be) is called the probe increment (or the probe size, or even just "the probe", for short. Thus the "re-hash index value" is either the next location, or the kth next location. If this location is full, but the table isn't, we keep looking by using the same re-hash function to re-hash further, as many times as needed until an empty space is found or we have nowhere else to look.
Question Once a collision takes place, and we begin to "probe" (notice the use of the word here as a verb) for an empty location, can we be sure that we will examine all remaining available locations in our search?
Answer Yes, under certain conditions. For example:
Example This example shows how the probe may fail if TABLE_SIZE and the probe increment are not relatively prime. First, take a look at the following diagram and note that it represents a hash table of TABLE_SIZE 10, which is full except for the location with index 1.
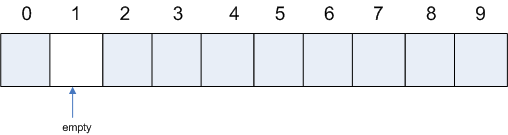
Suppose that hash(someKey) = 4, the index of a location which is already occupied, and suppose that we take
new_index = (old_index + 4) % 10
as our re-hash function. Then the sequence of values we look at is
8 2 6 0 4 8 2 ...
In other words, we fail to find the one remaining empty location. Note that we are not guaranteed to do so, since the probe increment and TABLE_SIZE are not relatively prime.
On the other hand, if we choose as our re-hash function
new_index = (old_index + 3) % 10
in which the probe increment and TABLE_SIZE are relatively prime, then the sequence of values we look at is
7 0 3 6 9 2 5 8 1
and we do indeed find the one remaining empty location. On this occasion, we actually had to run through all locations to find the empty one. This may or may not happen, of course, depending upon where we start.
So, we can set up a hash table, populate it, and then use it to retrieve the information that it contains. The next question is this: How do we handle deletions from the table, and inserting new values after the initial table setup?
And using a vector or array as originally suggested with "open addressing" causes no new problems when adding new values, provided there have been no deletions. But deletions themselves, and new insertions after there have been deletions have to be treated carefully.
The question centers around the problem that is caused by the deletion of a value from "somewhere in the middle" of a "hash sequence". Then we will not be able to find a value following the deleted one in the sequence unless we introduce a special marker to indicate a location from which a value has been deleted. Such a location is now free to receive another element, but must not be used to terminate a search. Hence the insertion and retrieval algorithms must deal differently with these locations.
One of the major problems with hashing is that it is generally not easy to retrieve hash-coded-and-stored data in any specific other format that might be required, such as alphabetical order, for example.
Our discussion of hashing was motivated by the desire to have a container for which insertion, deletion and retrieval were all O(1). If we have a hash function that never produces duplicates (collisions), or if the table size is very large compared to the expected number of data values to be stored in it, then we have achieved our goal. In general, in practice, however, this ideal is rarely achieved. The performance characteristics of open addressing using linear are summarized in the table shown below, in which
| Hash Table Performance (average number of probes) | ||
|---|---|---|
| Kind of Table | Successful Retrieval | Unsuccessful Retrieval |
| open addressing,
with linear probes |
½ (1 + 1/(1-λ)) | ½ (1 + 1/(1-λ)2) |
An interesting "parlor game" to try when you're out in a crowd of people (depending on the people, of course) is to suddenly ask, "I wonder if any two of us have the same birthday. Who wants to bet?" The question then becomes, "What are the chances?" Somewhat counter-intuitively, it turns out that you don't need as many people as you might think to have a pretty good likelihood of two of them having the same birthday. [That's the same birthday, note, not the same birthdate.]
In fact, the probability that n people all have different birthdays is
(364/365)(363/365)(362/365) ... (365-n+1)/365
and this product becomes < 0.5 as soon as n >= 23. Thus with at least 23 people in a room, there is a greater than 50% chance that two of them will have the same birthday.
What does this have to do with hashing? Well, if you have a hash table of size 365 into which you are placing people using their birthdays as keys, by the time you have only a couple of dozen people stored you have a greater than 50-50 chance of having a collision.
Or, more generally, one can interpret it this way: If you have any hashing problem of reasonable size, you are almost certain to have collisions.