Heaps

What is a heap?

A heap is a complete binary tree, each of whose nodes contains a key which is greater than or equal to the key in each of its children. Actually, this is technically a "maximum heap"; if we replace "greater than or equal to" with "less than or equal to", we get the definition of a "minimum heap".

Note that this use of the term heap has absolutely nothing to do with the other meaning of the word heap, which in that context was another term for "free store". Two words that have the same spelling or pronunciation but different meanings are called homonyms. Here are some other examples in which the sound is again the same, but at least the spelling is different: so and sew; do, dew, due; grate and great.

Thus we may say that a heap satisfies two properties:

1. A "shape property" (that is, it's a complete binary tree)
2. An "order property" (the value in a node is "optimal" with respect to the values in all nodes below it)

What are some uses for heaps?

• Heaps are ideal for implementing priority queues, which should not be surprising if you just think about the definition of a heap for a moment. For one thing, we can regard the root element as being the one of "highest priority", since this will be either the "largest" value (in the case of a maximum heap) or the "smallest" value (in the case of a minimum heap).
• Heaps also give us another sorting algorithm, called heapsort, which you should compare with selection sort, and for which the pseudocode (for sorting the values in a heap) looks like this:

  while not finished (while heap not empty)
      Remove root element and put it in its place
      Re-heap the remaining elements
  

  This is a O(n*log n) algorithm, and, unlike quicksort, it is guaranteed not to degenerate to O(n²). However, the algorithm begs a couple of questions:
  • How do you get a heap in the first place?
  • How do you "re-heap" after an insertion or deletion has been applied to a heap?

In order to deal with this question we introduce a new way of representing binary trees.

Non-linked representation of binary trees

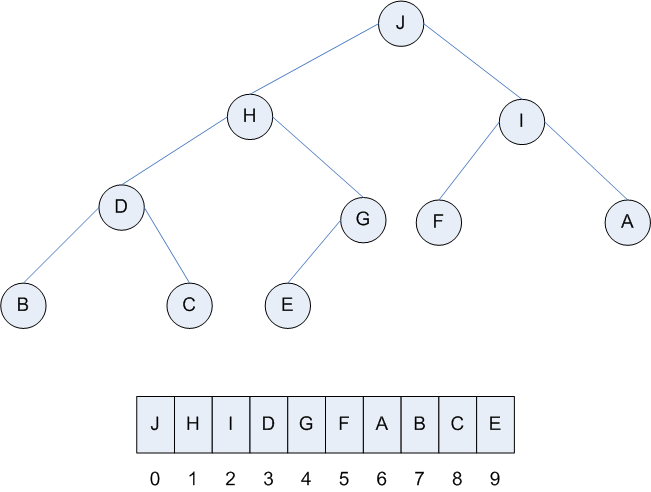
Study the binary tree shown below, and the array (or vector) that immediately follows it and contains the same values:

Note that although this binary tree happens to be a heap, it could be any kind of binary tree. That is, we could use this kind of representation for any of our binary trees; it's just that it turns out to be particularly convenient for heaps. You should make the following observations:

• If we place the values from the tree into a vector via a level-order traversal, then we have the following pattern:

  The children of the value at index 0 are at indices 1 and 2.
  The children of the value at index 1 are at indices 3 and 4.
  The children of the value at index 2 are at indices 5 and 6.
  The children of the value at index 3 are at indices 7 and 8.
  ... and so on, or, in general ...
  The children of value at index i are at indices 2i+1 and 2i+2.
  

  And, going the other way ...

  The parent of the value at index k is at index (k-1)/2.
  

• Also, since our example is a heap, it is of course a complete binary tree. This means that there are no "gaps" (i.e., "missing values" or "empty spots") in the vector representation. If we use this form of representation for some other kind of binary tree and there are such spots, we can us a special symbol (say '~', for character values) to mark them.

Now that we know what a heap is, and how we are going to represent it, it's time for the usual questions:

• Supposing we have an arbitrary vector of values, how do we turn it into a heap?
• Once we have a heap, how do we add a new value to the heap, while ensuring that the structure retains its heap properties (shape and order)?
• Once we have a heap, how do we delete a value from the heap, while ensuring that the structure retains its heap properties (shape and order)?

Though it seems natural to ask the above questions in the order given, it turns out to be convenient to answer them in the opposite order. These pictures illustrate the heap algorithms we need.

• Deletion So, note first that the element we delete from a heap is always the root element, which simplifies our discussion of heap deletion. Why should this be? Well, the whole rationale of the heap structure is to have the "optimal" value (maximum or minimum, say) at the root and hence "easily accessible". The idea behind deletion is thus to delete the root element and then make sure that what's left behind is again a heap, so that the "next most optimal element" will be in the root position of the revised heap.

  The way we perform deletion is to first overwrite the root value with the "most remote" value in the tree (last value in the vector). This retains the shape property, but destroys the order property. So, we have to move this value down through the tree by exchanging it with one of its children until we reach a point where the order property, and hence "heapness", has been restored. This process is called "re-heaping down", and its pseudocode looks like this:

  Algorithm ReHeapDown
  --------------------
  if currentNode is not a leaf
      Set maxChild to index of child of currentNode with larger value
      if value at currentNode < value at maxChild
          Swap value at currentNode with value at maxChild
          ReHeapDown starting at maxChild
  

• Insertion When inserting into a heap, we begin by adding the new element as the rightmost element on the bottom row of the tree (i.e., as the last element of the vector. This preserves the shape property, but again (in all likelihood) destroys the order property. This time, we need to move the value up the tree until it reaches the point where the order property, and hence "heapness" is restored. This process is called "re-heaping up", and its pseudocode looks like this:

  Algorithm ReHeapUp
  ------------------
  if value at currentNode > value at parent node
      Set parentNode to index of parent of currentNode
      Swap value at currentNode with value at parentNode
      ReHeapUp starting at parentNode
  

• Building Starting with a complete binary tree (i.e., a tree that has the appropriate shape for a heap) and "building" it into a heap (i.e., giving it the "order property" as well) is a "bottom up" process. And this process is based on the following observation: If we have two trees, a "left" one that is full, and a "right" one that is complete, and both are already heaps of the same height, then joining them at a root node in that left-right order will only require a "re-heap" down to restore "heapness". Thus, the pseudocode for building a heap looks like this:

  Algorithm BuildHeap
  -------------------
  for each index from first non-leaf back up to root (in reverse-level-order order)
      ReHeapDown starting at that index