| Assorted images |
| Klein Bottle |

|
This Klein bottle was traced using POV-Ray. It's built up from torus sections, and (thought it doesn't really show) it is hollow, with nonzero wall thickness. Thus, it refracts "light" like a real glass model would. Next best thing to really being able to blow glass, I guess...
(When I was in graduate school, there was a brief fad for knitting Klein bottles. As I recall, what the knitters did was to use a crochet hook to pull the wool through already-knitted parts, and then keep knitting on the other side. I think that Manifold had an article on knitting surfaces once, but I don't know when.)
|
|
| Skolem Crossbones |
Not a raytracing at all. Just a bad pun.
A "Skolem labelling" of a graph is a labelling using 2 copies each of 1,2,3,...,n (optionally one 0 as well) so that the two copies of each integer n are at distance n in the graph. That's all...
|

|
|
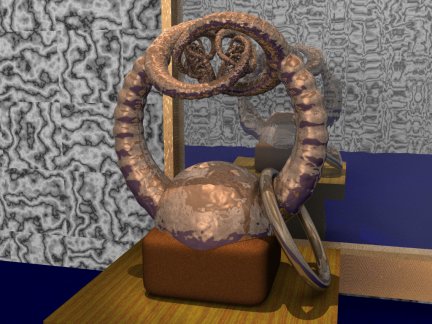
| Alexander's Horned Sphere |
|
Imagine a sphere (bottom center) that grows two horns. The points approach each other; then each of them grows two horns in turn. The pairs nearly interlock; then each of them grows two horns....
The final structure could shrink back into itself like a snail's horns; so it's homotopic to the original sphere. However, a loop of string around one of the main horns cannot be removed in a finite number of moves; so it's embedded "wildly" in space.
|
|
| Hopf Fibration: Homage to Georgia O'Keefe |
|
The Hopf fibration is a way of packing a 3-sphere (spherical 3-space) with circles. For us, it's often
convenient to think of a 3-sphere as an ordinary 3-dimensional space compactified by putting a single point at infinity that every straight line gets to if you extend it far enough. (Our universe may really have this structure, on a very large scale.) However, this representation, while it makes it easy to imagine and draw, hides the fact that all the circles in the fibration are really great circles, like the Equator or a meridian on the Earth.
In reality, all the circles are the same: in the geometry of the 3-sphere they are all "straight lines", and a suitable rotation will take any one of them onto any other while preserving the pattern. No representation in a flat space will show this fully. However, you can see in this picture (which shows only two bands of the fibers; the full set of fibers fills the whole space) that every circle is linked with every other circle. They also pack the space smoothly; two circles that are close at one point are close everywhere. What's really interesting is that the circles are indexed by the points of an ordinary 2-sphere! That is, the 3-sphere "is" a sphere of circles in the same way that a torus is a circle of circles. There is a lot of very deep and important mathematics related to this fact.
In this representation, the circle that passses through the point of the sphere that we have chosen to be "at infinity" becomes a straight line, while the "opposite" circle encircles it symmetrically. These are related rather like the poles and equator of the earth, except one dimension higher.
The bands of fibers shown were chosen partly to represent the nature of the fibration and partially for aesthetic reasons. The silver band runs between opposite circles of the fibration along a "great circle", like a meridian on the earth's surface; the gold band runs around part of a small circle (like, say, the Arctic Circle). The overall pattern is reminiscent of Georgia O'Keefe's paintings of calla lilies and other flowers.
|

|
|
| From Minus Infinity to Infinity |

|
This image represents a reflective sphere rolling along an infinite helical ramp, from minus infinity to infinity (or possibly the other way?). Only a tiny bit of the ramp can be seen directly, but the whole thing (except a very small section) can be seen in the reflection. The resulting curve is slightly reminiscent of an integral sign, recalling the title again.
|
|
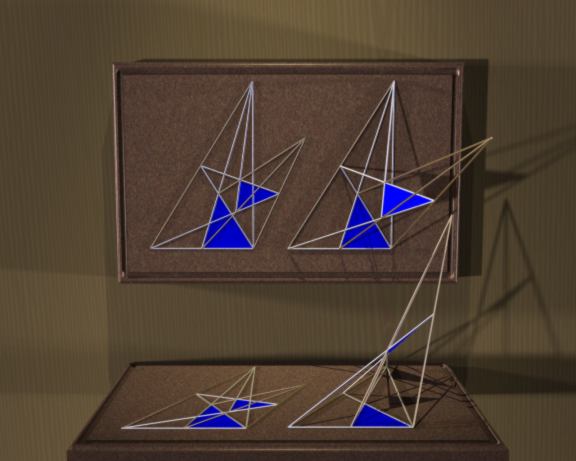
| Desargues' Theorem |
|
Deasargues' theorem says that if two triangles ABC and A'B'C' are perspective - that is, the three lines AA', BB', and CC' all meet at a point O
(think of a "vanishing point" in art) - then the points where corresponding edges meet
(L where AB meets A'B', M where AC meets A'C', and N where BC meets B'C') lie on one line.
This theorem has several fascinating properties. Firstly, it is a result which can be stated in projective geometry, a geometrical system in which concepts such as "length" and "angle" have no meaning, and every pair of lines in the plane meets exactly once. What would have been "parallel lines" meet at a "point at infinity" (think of railway lines appearing to meet at the horizon, especially if you live on the Prairies.) Desargues' theorem uses this concept of "meeting at infinity" to handle special cases.
There are many different projective geometries, including some with only finitely many points and some with infinitely many. Desargues' theorem is not a theorem of all of them. It is true in many of the most common ones, including the one obtained from the real Euclidean plane by adding a line of points at infinity.
|
The axioms of a projective plane are simple:
- Every point is on at least two lines
- Every line is on at least two points
- Every two lines have a point in common
- There exist four points, no three on one line
From these axioms we can prove that every two points have a line through them, and that there exist four lines, no three through one point. It follows that
- Every line is on at least two points
- Every point is on at least two lines
- Every two points have a line in common
- There exist four lines, no three on one point
is also a set of axioms for projective geometry. This symmetry between points and lines is called duality . Desargues' theorem is self-dual; interchanging "point" and "line" gives an essentially equivalent theorem.
|
|
|
One very odd feature of Desargue's Theorem is that the two-dimensional case is moderately hard to prove directly! However, the three-dimensional case is almost trivial - the
points L,M,N obviously lie in the plane of triangle ABC, and also in the plane of triangle A'B'C'; thus they lie (ta-daaa!) on the line of intersection of those planes. Moreover, perhaps the easiest way to prove the planar case is by introducing a third triangle in a three-dimensional construction. What is this trying to tell us?
Well, this turns out to have deep meaning in projective geometry. As I mentioned above, Desargues' theorem does not hold in every projective plane. It turns out that if any one of the following is true for a particular projective plane, so are the others:
- The projective plane has a coordinate system
- The projective plane can be extended to a projective 3-space
- Desargues' theorem holds
So Desargues' theorem is, in a sense, equivalent to the existence of a third dimension! Had the authorities of Edwin Abbott's "Flatland" been competent geometers, perhaps "Mr. A. Square" should have attempted to prove the existence of the Third
Dimension that way!
|
|
| Proof Without Words |

|
This is a real Canadian advertisement, except for the caption.
|
|
| Complex Slide Rule |
|
This raytracing illustrates (in a slightly fanciful "steampunk'' style) a slide rule for multiplying complex numbers .
A simple "complex slide rule'' could be built using a logarithmically labelled plane and a transparent overlay (say a sheet of paper and an acetate photocopy.) According to Whythe the first known planar slide rule for complex numbers was devised by J. W. M. DuMond in the 1920's, though there is no evidence that it was marketed. Faber-Castell patented a calculating device based on roughly the same concept, and with additional features, in 1952 . It was manufactured and sold between 1955 and 1960; somewhere between 100 and 200 appear to have been sold.
Identifying all complex numbers that differ by a multiple of 2 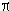 i, we obtain an infinite cylinder as the quotient space, and the logarithm can be considered as a single-valued function from the nonzero complex numbers onto this cylinder. It is (a section of) this cylindrical Riemann surface that is used here. i, we obtain an infinite cylinder as the quotient space, and the logarithm can be considered as a single-valued function from the nonzero complex numbers onto this cylinder. It is (a section of) this cylindrical Riemann surface that is used here.
In the abstract, we could perform both identifications at once, identifying z with every point of the form z + 2n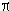 i + mlog 10. This would give us a "toral slide rule'' with no wraparound problems. Unfortunately, no three-dimensional model would slide correctly; in four dimensions it could be done. i + mlog 10. This would give us a "toral slide rule'' with no wraparound problems. Unfortunately, no three-dimensional model would slide correctly; in four dimensions it could be done.
Faber-Castell included in their 1952 patent an alternative design with a transparent cylinder, very similar to that illustrated here . There is no evidence that Faber-Castell ever produced such an instrument; however, in 1956 Arnold Sander independently rediscovered the idea. He not only described it in a short article in Mathematisch-Physikalische Semesterberichte , but he even made a prototype, of which a photograph is included in his note.
Unfortunately, this "lamp chimney'' mechanism is not really practical; it is too hard to read one scale through another. Around 1960, D. J. Whythe adapted the "Fuller'' mechanism, which had been used for cylindrical slide rules since the nineteenth century, for a complex slide rule which was marketed for some years by W. F. Stanley, in England. The Fuller mechanism used only one scale, supplemented by one fixed and one movable pointer. The original Fuller slide rules bore a very long linear scale wrapped into a helix, thereby allowing a portable instrument to have a scale many meters long, and several decimal places of precision.
Ironically, however, the precision of Whythe's instrument was only equivalent to that of a pocket slide rule a few inches long; results would be valid to only two significant figures. This weakness is shared by all known complex slide rule designs if built to a practical size (though a certain amount of improvement is possible). It is thus not surprising that complex slide rules never became very widespread.
For instructions on building your own, go here . [Now, how would you design a quaternionic slide rule?]
|

|
|
|
|
To get your own copy of POV-Ray, go to ftp.povray.org or one of their various mirror sites.
|
Back to Robert Dawson's home page Back to Robert Dawson's raytracing page
|








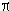 i, we obtain an infinite cylinder as the quotient space, and the logarithm can be considered as a single-valued function from the nonzero complex numbers onto this cylinder. It is (a section of) this cylindrical Riemann surface that is used here.
i, we obtain an infinite cylinder as the quotient space, and the logarithm can be considered as a single-valued function from the nonzero complex numbers onto this cylinder. It is (a section of) this cylindrical Riemann surface that is used here.