Making a complex slide rule

This page contains all the information you need to make your own complex number slide rule. You can choose between three styles: the rather primitive planar model (DuMond, 1920), the "lamp-chimney" style (Faber-Castell, 1952; Sander, 1956), still easy to build but harder to use; and the "Fuller-type" slide rule (Whythe, 1961).

The basic raw material is this image. Click on it to download a GIF version.

Legal disclaimer

By downloading the image to the left you acknowledge that it is not designed or intended for use in the design, construction, operation or maintenance of any nuclear facility, spaceship, or time machine.

NOTE: If you want to make your own or are curious, here's how it was made. As can be shown fairly easily, all loci of log(z) where z has a specified equal real or imaginary part are translates of the graph of y=log(sec(x)). I used Corel Draw to create one copy of the graph using cubic beziers, and then combined many copies in different colors and line weights. Another approach would be to cut out one card template and trace along the edge.

This is essentially the same file used as a cylindrically-mapped image pigment file in the raytraced image here. It will probably be larger than you need, but can easily be scaled with Photoshop, PhotoPaint, the GIMP, or any other decent bitmap manipulation program. (If you know about "conformal maps" in complex analysis, you may wonder whether rescaling has to preserve aspect ratios. It doesn't; you can make your scale proportionally wider or taller.)

The DuMond slide rule

Print one copy on heavy paper and a second copy onto an acetate sheet. That's it!

To find a complex number: locate its real part on one of the black vertical axes and its complex part on one of the red vertical axes. Follow the transverse lines; where they intersect is the complex number you want. Note that one black axis represents positive real parts, the other negative real parts; and similarly for the red axes.

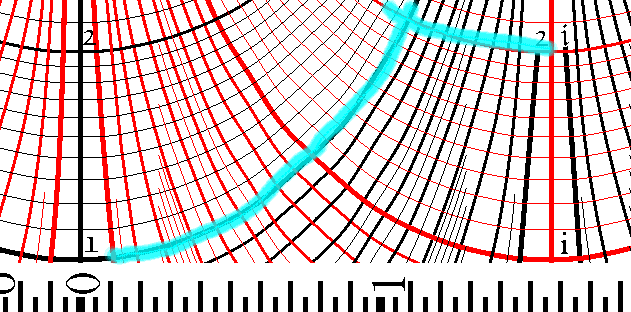This picture shows how to find the complex number 1+2i.

To multiply complex numbers: Overlay the transparent sheet on the opaque sheet. The sheets should have the same orientation, and the point 1 of the transparent sheet should lie over the point on the opaque sheet reprenting one of the numbers you want to multiply. Now find the other factor on the transparent sheet. The point directly below it on the opaque sheet represents the product. (If you're off the edge, use the point 10 instead of 1. People using ordinary (straight) slide rules sometimes had to do this too! Circular slide rules didn't have this problem.)

To divide complex numbers: Align the divisor on the transparent sheet with the dividend on the opaque sheet. The point 1 on the transparent sheet aligns with the quotient.

To find the absolute value: Align the green line on the transparent sheet with your number. Where it crosses the black (positive real) axis on the opaque sheet is the absolute value.

To find the argument: Align the black axis on the transparent sheet with your number. Where it crosses the scale numbered 0,1,...6 at the bottom of on the opaque sheet is (one value of) the argument (in radians of course).

The lamp-chimney slide rule

Get a length of cardboard mailing tube (maybe 5 cm outer diameter by 15cm long but this is not crucial.) Scale the image to fit it exactly (with the straight lines running along it, though it would work, more or less, the other way too. Print it onto a sheet of light paper, cut it to size, and stick it onto the tube.
Now print another copy onto an acetate sheet, maybe a half millimeter wider. Cut it to size and use transparent tape to form it into a slightly loose cylinder around the tube.

The Fuller-Whythe slide rule

For this you will not need to print on acetate, but as well as a piece of mailing tube you will need a length of good-quality wooden dowel a bit more than twice as long as the tube, a few scraps of wood, and some basic tools. A drill press and scroll saw would help a lot.

Prepare two discs of wood that fit into the ends of the mailing tube, with centered holes that allow the cylinder to slide smoothly on the dowel. Make the following (use your imagination!)

An end cap to fit the dowel
An end piece to fit the other end of the dowel that extends sideways as far as the edge of the cylinder, with a thin wooden pointer as long as the tube attached.
A sliding piece that moves along the dowel, also extending out to the width of the cylinder, with a similar pointer attached.

Assemble these so that the cylinder and slider can slide on the dowel, the caps are glued in place, and the two pointers can meet in opposite directions next to the cylinder.
To use this slide rule, put the tip of one pointer at 1 and the tip of the other pointer at one of your factors. Now move the cylinder so the other factor is at the tip of the first pointer; the tip of the second pointer will be at the product.

Other things to try

You could increase the precision by cutting the scale at the green line and resizing. In the other direction, if you can keep track of sign in your head (as an old-fashioned slipstick wizard kept track of the order of magnitude) you could also cut in the opposite direction, using only one red and one black axis. The same point will now represent 2-i and -2+i. (If you make one scale like this and one from the original image, they will work like the C and A scales on an ordinary slide rule and let you compute squares and square roots!)

This idea can even be taken further; if you can keep track mentally of which quadrant of the complex plane you are in you can double your effective size again. If you cut vertically on either side of the real axis, halfway out to either imaginary axis, and rescale, you can wrap the resulting image into a cylinder, and the contours of the real part will meet up neatly with those of the imaginary part. As the pattern can be rescaled arbitrarily in the longitudinal direction, it is posisble to quadruple the effective linear dimension of the rule! Had Whythe done this, his instrument would have had a precision at least as good as that of a standard 12" slipstick. (though it would have been a little mindbending to use) You should probably make a black-and-white copy of the scale before trying this, as the same set of contours serves for both real and imaginary parts, so the color coding is now meaningless.

Back to Robert Dawson's home page ............Back to Robert Dawson's raytracing page ............Back to the raytraced image ............Back to the top of this page