Note: This is available online in three forms. For each one you will need the associated viewer!
These can be downloaded free of charge.

en français
| Contents | ||
| What math will I need in university? | ||
| What is calculus? | ||
| Why is calculus important? | ||
| What background will I need? | ||
| What is taking university calculus like? | ||
| HELP! I have to write a placement test! | ||
| HELP! They want to take away my calculator! | ||
|
Get the booklet "Preparing for University Calculus" Note: This is available online in three forms. For each one you will need the associated viewer! These can be downloaded free of charge. |
||
| Find out more about the booklet here | ||
| Get the booklet in PostScript format. | Get the booklet in PDF format |
Lire cette page  en français |
| Read the PS version with GhostView . You will need to run Ghostview once after installation, to configure it, before viewing booklet! | To read PDF files,
|
|
Some departments may teach their own courses in calculus, linear algebra, or statistics. In this case, you may not need to take the standard first-year courses offered by the mathematics department.
Basic ideas of calculus include the idea of limit , derivative , and integral . The derivative of a function is its instantaneous rate of change, with respect to something else. Thus, the derivative of height , (with respect to position) is slope ; the derivative of position , (with respect to time) is velocity ; and the derivative of velocity (with respect to time) is acceleration.
The integral of a function can be thought of as the area under its graph, or as a sort of total over time. Thus, the integral of slope is (up to a constant) height ; the integral of velocity is, up to a constant, position; and the integral of acceleration (with respect to time) is velocity. As you may have guessed, integrals and derivatives are related, and are in a sense opposites.
Now, many functions (though not all) can be represented by algebraic expressions. For instance, the area of a circle is related to its radius by the formula A=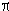 r2; and the distance that a body falls in a time t, starting at rest, is given by
x = 1/2 a t2. Given such an expression, calculus allows us to find expressions for the integral and derivative of the function, when they exist.
r2; and the distance that a body falls in a time t, starting at rest, is given by
x = 1/2 a t2. Given such an expression, calculus allows us to find expressions for the integral and derivative of the function, when they exist.
Physics, astronomy, mathematics, and engineering make particularly heavy use of calculus; it is difficult to see how any of those disciplines could exist in anything like its modern form without calculus. However, biology, chemistry, economics, computing science, and other sciences use calculus too. Many faculties of science therefore require a calculus course from all their students; in other cases you may be able to choose between, say, calculus, statistics, and computer programming.
It should be understood that there is more to mathematics than calculus. Some mathematics courses may have first-year calculus as a prerequisite to ensure that students taking those courses have a certain level of mathematical sophistication, but may not actually use calculus at all.
Note that some choices of math course at the Grade 10 or Grade 11 level may make it difficult or impossible for you to take precalculus math. Do not throw away your options by a careless choice of courses!
This is not a course that can be passed by just memorizing everything; you have to understand it. This won't happen instantly, and the instructor cannot make it happen; you have to do that yourself, and be an active participant in the course. If you make this effort consistently through the term, you will find that it pays off.
The course material consists of a rather small number of big ideas, and a moderate number of formulae you will need to know, not hundreds of short cuts and special rules. A common mistake, especially with word problems, is trying to learn one ``plug-in'' rule for each different kind of problem that you might encounter. Don't do that; instead, try to understand the underlying patterns.
Here are the stages by which you will learn and master a new idea in calculus.
 | Yourself. If you are falling behind and not putting plenty of time in studying - say five or six hours outside class per week for each course - the solution may be as near as your desk and textbook. |
 | Your textbook contains hundreds of worked examples, and thousands of problems. Usually, about half of them have answers in the back of the book; and you may be able to buy a study guide that shows the working of those problems in more detail. You can also get other books such as ``Schaum's Outline of Calculus'' containing more worked problems. |
 | Your instructor will have office hours during which you can go for help. Try to figure out ahead of time what you need help with; you will get more out of the visit. |
 | Discuss your problem with your classmates. This is not the same thing as copying their assignments, of course! University penalties for cheating are severe, and can include expulsion. |
 | You might want to hire a tutor . Do not try to get the tutor to do your assignments for you; you will not be able to bring the tutor into the exam with you! Get the tutor to make sure you understand the material. |
 | Your university may have a math learning center , group tutoring sessions, or other resources that you can use. Take advantage of them! |
 | Your university or student union may well have workshops on effective studying, effective note-taking, exam nerves, etc. There will also be counselling available for other problems that might interfere with your study. |
This is to stop students from starting calculus without adequate preparation and then falling behind and failing. Experience has shown that most students who start calculus without adequate preparation do fail.
The test is often multiple-choice so that it can be graded as quickly as possible. It will generally be closed-book and written without a calculator (see the next section). Because success in first-year calculus requires a fairly high level of preparation, and because the test covers some very elementary (but important) material, the pass mark may be higher than 50%. You will probably have to write the test at or before the beginning of term; find out ahead of time what the rules are at the university you plan to attend.
 |
If your calculus course has a no-calculator policy, the questions will be designed so that a calculator is not needed. It would be unreasonable for the professor to ask you to compute |
 |
In a situation where calculators are not permitted, any expression that does not have a well-known simplification may always be left as it is. Thus, for instance, while you are expected to know that 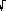 25 = 5, and that log10 1000 = 3, you may always leave (eg) 25 = 5, and that log10 1000 = 3, you may always leave (eg) 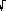 17 or ln(1000) in those forms. Now, that is even easier than using the calculator! 17 or ln(1000) in those forms. Now, that is even easier than using the calculator! |
 |
Do note, however, that you would generally be expected to simplify (eg) 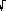 17/ 17/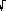 17 17 |
 |
Even if your calculus course does allow calculators, you will
often be required to give, as an answer, an algebraic expression
involving integers. For instance, you might be asked: ``Give
the answer as an expression of the form 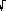 b/c where b and
c are integers.'' It is far more important, for the purposes of
calculus, to know that sin( b/c where b and
c are integers.'' It is far more important, for the purposes of
calculus, to know that sin(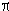 /4) = /4) = 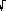 2 / 2 than to know that
it is approximately equal to 0.707. 2 / 2 than to know that
it is approximately equal to 0.707.
|
| To report errors on the web page or in the booklet contact Robert Dawson . For any other enquiry please contact the admissions office or mathematics department at the university concerned. | |
Participating Departments |
|
| Acadia University, Department of Mathematics and Statistics | |
| Dalhousie University, Department of Mathematics, Statistics and Computing Science | |
| Mount Saint Vincent University | |
| Saint Marys University, Department of Mathematics and Computing Science | |
| Memorial University of Newfoundland, Department of Mathematics and Statistics | |
| Sir Wilfred Grenfell College, Department of Mathematics | |
| Saint Francis Xavier University, Department of Mathematics, Statistics and Computer Science | |
| University College of Cape Breton | |
| University of New Brunswick (Fredericton), Department of Mathematics and Statistics | |
| University of New Brunswick (Saint John) | |
| University of Prince Edward Island, Department of Mathematics and Statistics | |